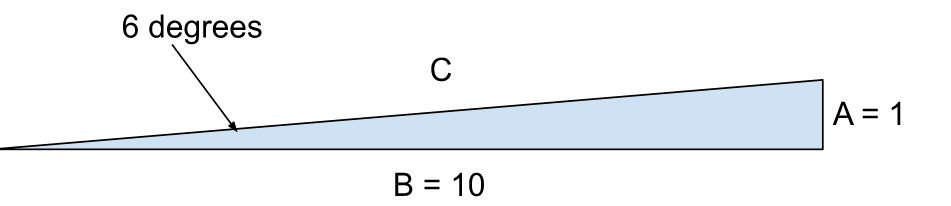
The Small Angle Rule
To a good degree of accuracy, the height of an angle of 6 degrees is one-tenth the length of either side. The rule can be expanded by multiples of 6 for larger angles. This is useful for approximating tidal influence. What this is saying is the current must push you 0.1 nmi off course laterally before the compass would show a 6 degrees change in heading.
This is the idea that for every 6 degrees on a right triangle, the shortest side is roughly 1/10 the length of B. Given a 3-degree room for error on bearing fixes in either direction, this gives a 10% room of error for an object 1 nm away. This works out to roughly 200 yards of error or 183 meters. Therefore, with 6 degrees of an error on two bearings to objects 1 nautical mile away, that makes the margin of error roughly 400 square yards.
| Angle | A/B or A/C | A/C % Error | A/B % Error |
|---|---|---|---|
| 3 | 0.05 | 5 | 5 |
| 6 | 0.1 | 5 | 5 |
| 12 | 0.2 | 4 | 6 |
| 18 | 0.3 | 3 | 8 |
| 24 | 0.4 | 2 | 11 |
| 30 | 0.5 | 0 | 16 |
