Distance Off
Below are different methods of using objects on shore to determine your distance from it. This distance, plus a bearing will yield a fix.
Horizontal Angle
Long Distance off (in miles) = 60 * Target width (in miles from the chart)/Target angle (in degrees from your position)
Example: A bay 1 mile across that appears to be 6 degrees wide = 60(1/6)= 10 miles off.
This is an example of the small angle rule.
Pretend the graphic below is seen from a birds-eye view.
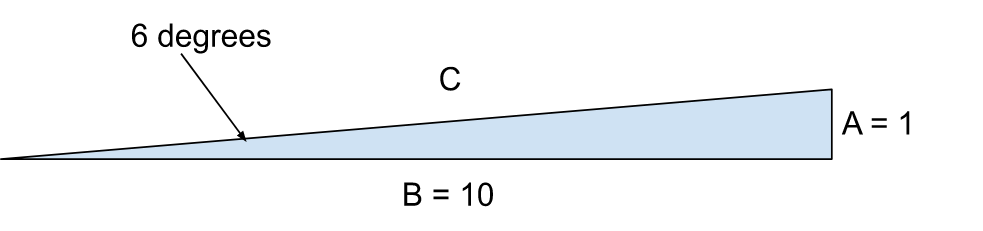
Short Distance off (in miles) = Target width (in feet) / 100*target angle (in degrees)
Vertical Angle

This is the same as the horizontal angle just flipped 90 degrees.
Short Distance off (in miles) = Target height (in feet) / 100*target angle (in degrees)
Pretend the graphic is seen at ground level and side A is the height of the object.
Winking
This is based on the idea that it is roughly a 1:10 ratio between the width of one's eyes and the length of their arm. By looking at your finger and alternating winking eyes, you can get roughly a 6-degree angle. The distance between two points you can identify on shore would be 1/10 how far out you are. Or, multiply the distance of the onshore spots 6 degrees apart by 10 and you'll get roughly your distance out. You can take this information and plug it into the above formulas.
Doubling The Bow
Pick a course and hold the course at a constant speed. Find any mark or bearing on the shoreline. 45 degrees is a convenient angle. Time how long it takes for this mark to be 90 degrees of the beam. Multiply the time by the speed to get the distance travelled.
This distance traveled is approximately how far away you are form the object being tracked.
If the mark takes 5 minutes to reach the beam and you are going 6 knots then:
D = V*T
D = 6 nm/1hr * 5 min/1 hr * 1 hr/60min
The 1 hours cancel leaving.
D = 6 nm/1hr * 5 min/60min
D = 6 nm/1hr * 0.0833 hrs
Hours cancel.
D = .5 nm
